1. 비지도 학습 개요
- 전체 프로세스(CRISP-DM)

- 업무 이해
- 비즈니스 관점에서 프로젝트의 목적과 요구사항을 이해하는 단계
- 업무 목적 파악, 상황 파악, 데이터 마이닝 목표 설정, 프로젝트 계획 수립
- 데이터 이해
- 분석을 위한 데이터를 수집하고 데이터 속성을 이해하는 단계
- 초기 데이터 수집, 데이터 기술 분석, 데이터 탐색, 데이터 품질 확인
- 데이터 준비
- 분석을 위해 수집된 데이터에서 분석기법에 적합한 데이터를 편성하는 단계
(많은 시간이 소요될 수 있음) - 분석용 데이터셋 선택, 데이터 정제, 분석용 데이터셋 편성, 데이터 통합
- 분석을 위해 수집된 데이터에서 분석기법에 적합한 데이터를 편성하는 단계
- 모델링
- 다양한 모델링 기법과 알고리즘을 선택하고 모델링 과정에서 사용되는 파라미터를 최적화하는 단계
- 모델링 기법 선택, 모델 테스트 계획 설계, 모델 작성, 모델 평가
- 평가
- 모델링 결과가 프로젝트 목적에 부합하는지 평가하는 단계
- 분석 결과 평가, 모델링 과정 평가, 모델 적용성 평가
- 전개
- 모델링과 평가 단계를 통해 완성된 모델을 실무에 적용하기 위한 계획을 수립하는 단계
- 모델 모니터링, 모델 유지보수 계획 마련, 프로젝트 마무리
- 비지도 학습 특징
- 학습 시 x만 사용
- x 안에서 패턴 인식 문제
- 지도 학습에서 target으로 사용했던 y 없이 학습하여 알아서 예측, 추론 진행
- 후속 작업 필요(비지도 학습으로 끝나지 않음)
- [차원축소] 고차원 데이터를 축소하여 새로운 feature를 생성 ➔ 시각화, 지도학습 연계
- [클러스터링] 고객별 군집 생성 ➔ 고객 집단의 공통 특성 도출을 위한 추가 분석
- [이상탐지] 정상 데이터 범위 지정 ➔ 범위 밖 데이터를 이상치로 판정
2. 차원 축소
2.1. 차원의 저주
- 차원(dimension)
- 차원의 수 = 변수의 수
- 다양한 변수를 고려 ➔ 모델 성능 향상
- 예) 고객의 건강 상태 분석
- 키, 몸무게 (2차원) ➔ 기본적인 분석
- + 혈압, 체성분 지수, 나이 (5차원) ➔ 더 구체적인 건강상태 분석 가능
- 하지만 변수가 너무 많아지면?
- 크게 필요하지 데이터가 않은 데이터를 포함할 경우
- 모델이 학습하는 데에 오히려 방해가 될 수도 있음
- 또는 불필요하게 복잡한 모델이 생성됨

- 데이터가 매우 희박해짐
- 따라서 모델의 학습이 적절하게 되지 않을 가능성이 높아짐(이것을 차원의 저주라고 함)
- 고차원 데이터 문제 해결 방안
- 행 늘리기 ➔ 데이터 늘리기
- 열 줄이기 ➔ 차원 축소
- 차원 축소

- 다수의 feature (고차원) ➔ 새로운 소수의 feature (저차원)로 축소
- 기존 특성을 최대한 유지
- 대표적인 방법: 주성분 분석(PCA), t-SNE
2.2. 주성분 분석(PCA)
- 주성분 분석(PCA Principal Component Analysis)
- 변수(차원)의 수보다 적은 저차원의 평면으로 투영(Projection)
(고교 수학시간에 배운 정사영을 떠올리면 이해가 빠르다.)

➔ 평면1, 평면2 중 럭비공의 특징이 더 잘 반영된 것은 평면1이다.
- 어떤 평면으로 투영시킬 것인가?
- 정보의 특성을 최대한 유지하면서(분산을 최대한 유지) 차원을 축소한다.

- PCA 절차
- 학습 데이터셋에서 분산이 최대인 첫번째 축(axis)을 찾음.
- 첫번째 축과 직교(orthogonal)하면서 분산이 최대인 두 번째 축을 찾음.
- 첫 번째 축과 두 번째 축에 직교하고 분산이 최대인 세 번째 축을 찾음.
- ①~③과 같은 방법으로 데이터셋의 차원 만큼의 축을 찾음.
- 주성분 분석을 수행하면
- 각 축의 단위벡터를 주성분이라고 부름
- 각 축 별 투영된 값이 저장됨
2.2.1. PCA 사용하기
- 전처리: 정규화(scaling) 필요
- 주성분 결정시, 분산 비교(크기 비교)
- 스케일링 없이 PCA를 수행 ➔ 스케일이 가장 큰 변수에 영향을 가장 많이 받게 됨
# 주성분을 몇개로 할지 결정(최대값: 전체 feature 수)
n = x_train.shape[1]
# 주성분 분석 선언
pca = PCA(n_components=n)
# 만들고, 적용하기
x_train_pc = pca.fit_transform(x_train)
x_val_pc = pca.transform(x_val)
- PCA 문법
- 선언: 주성분의 개수(n) 지정
- 1 ≤ n ≤ feature의 수
- 생성 후 조정 가능
- 적용
- x_train으로 fit & transform
- x_val 데이터는 transform
- 결과는 numpy array가 됨
- 주성분의 개수 정하기
- 주성분의 개수를 늘려가면서 원본 데이터 분산과 비교
# 주성분 개수에 따른 시각화
plt.plot(range(1,n+1), pca.explained_variance_ratio_, marker = '.')
plt.xlabel('No. of PC')
plt.grid()
plt.show()※ .explained_variance_ratio_ ➔ 원본데이터의 전체 분산 대비 누적 주성분의 차이 비율
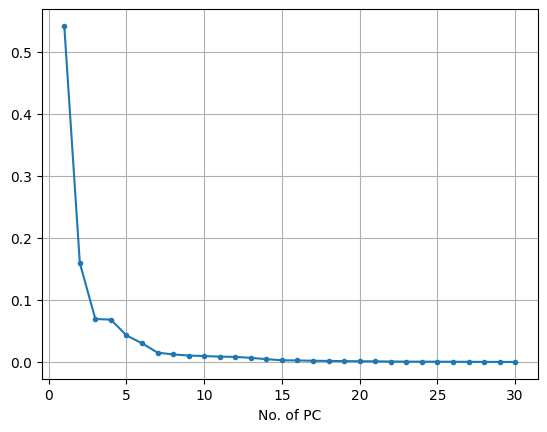
- 위 그래프의 형태가 팔꿈치의 형상과 닮아 'Elbow Method'라고도 부른다.
- Elbow Method(팔꿈치 지점 근방에서 적절한 값을 찾아라)

※ X = 3 지점까지만 의미 있는 y값 변화가 이루어지고 그 이후로는 변화량이 미미하다.
- X축의 값이 계속 증가해도, y축의 값의 개선 폭이 줄어 드는 지점
- Trade-Off 관계일 때, 적절한 지점을 찾기 위한 휴리스틱 방법
2.3. t-SNE
- PCA의 단점
- PCA → 선형 축소 방식
- 분산의 크기만 고려한 선형축소방식
- 저차원에서 특징을 잘 담아내지 못하는 경우 발생

- t-SNE
- 원본의 특성을 최대한 살리면서 축소하는 방법 필요
- 원본에서 가까운 거리의 점들은 ➔ 원본의 유사도 맵 생성
- 축소한 후에도 가깝게 만들자. ➔ 축소된 데이터의 유사도 맵

- 위 방법을 통해 두 맵의 오차를 줄이는 방향으로 축소된 데이터 조정이 가능하다.
- t-SNE 사용하기
- 전처리: 정규화(scaling)
- 꼭 필요한 것은 아니지만, 해주는 것을 권장
- 학습
- 고차원을 2 ~ 3 차원으로 축소
- 주로 데이터 시각화를 위해 사용됨
- 학습하는데 오래 걸림
from sklearn.manifold import TSNE
# 2차원으로 축소하기
tsne = TSNE(n_components = 2, random_state=20)
x_tsne = tsne.fit_transform(x)
# 사용의 편리함을 위해 DataFrame으로 변환
x_tsne = pd.DataFrame(x_tsne, columns = ['T1','T2'])
# 확인
x_tsne.shape
# 출력
# (569, 2)
요약: 차원 축소
| Focus | - 차원을 축소하여 새로운 feature 만들기 - 활용 - 고차원 데이터 시각화 - 지도학습으로 연계 |
| PCA | - 고차원의 특징(분산)을 최대한 유지 - 선형 방식 - Feature의 수 만큼 추출 가능 - 지도 학습에 유리한 방식 |
| t-SNE | - 고차원의 특징(유사도)를 최대한 유지 - 비선형 방식 - 2~3개로 축소 ➔ 시각화에 자주 사용됨 |
'에이블스쿨 6기 DX 트랙 > 일일 복습' 카테고리의 다른 글
| 딥러닝 4일차 (0) | 2024.11.04 |
|---|---|
| 딥러닝 1일차 (0) | 2024.10.30 |
| 성능 평가 (0) | 2024.10.17 |
| 데이터 분석 - 이변량: 범주 vs 숫자 (0) | 2024.10.04 |
| DAY 08. 데이터프레임 조회 (0) | 2024.09.20 |